
Previously confined to PC turn-based play, mobile free-to-play transformed 4x into sprawling persistent world MMOs. The combination was and continues to be electric; what other genre can admit to $1M LTVs? Each X, EXplore, EXpand, EXploit, and EXterminate invites an unparalleled level of feature width and depth. 1 Its LTVs are not driven only by spend depth but also by copious amounts of long-term retention. Like long, long-run retention.
The “10-year game” has gone from a CEO fairy tale to reality. A couple of weeks ago, Clash of Clans (CoC) celebrated its 10th anniversary by grossing over $480 million in the last year alone. But longer lifecycles present new and unexplored challenges. 4x faces a genre-level conundrum: given vertical progression and persistent worlds, what is the most effective way to manage server populations?
Shards
4x games typically funnel new players into “mirrored worlds” segmented by language and real-world region. Each shard shares a similarly sized population cap and “static” elements like progression speed or world map size. Tiny shards (< 10,000) like those in Star Trek Fleet Command create laboratories for experimentation and mistake. Even on 1M MAU, that translates to 500 parallel worlds or shards. On the other hand, a few games have instead opted for a single shard shared between all players. Managing single shards, like those in EVE and Dual Universe, is technically tricky, with over 200k DAUs sharing a single real-time and persistent server. Still, the shared sense of history from a single shard setup binds a community together in a way little else can.
Server persistence combined with vertical progression introduces unique time-based effects; additional doses of vertical progression increasingly stratify players across power levels. As the vertical progression cap increases, it becomes increasingly expensive for new players to win. For example, it may have taken 1,000 hours / $10,000 to reach level 100, but now takes 3,000 hours / $50,000 to reach level 150; “catch-up” is expensive for new players. Imagine starting a marathon hours after other competitors, only to find out the organizers have extended the finishing distance by several miles. And to be sure, extending vertical progression caps are a necessary condition for retaining elder players; nothing kills a game quicker than no new content.
Spent Cap Model
For any 4x game, consider the vertical ceiling or the max amount of progression as the sum of all individual durable timers (i.e., how long you have to wait to upgrade a building).
For most games, the vertical ceiling follows an exponential curve. Not only will leveling up a building require more and more time, but the total number of upgradeables increases as players progress. On the one hand, this suggests absolute vertical power increases exponentially.
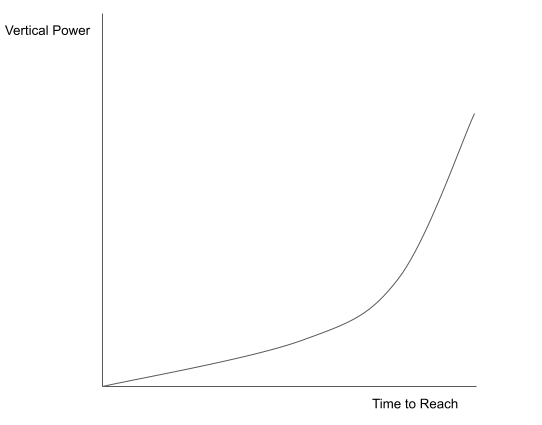
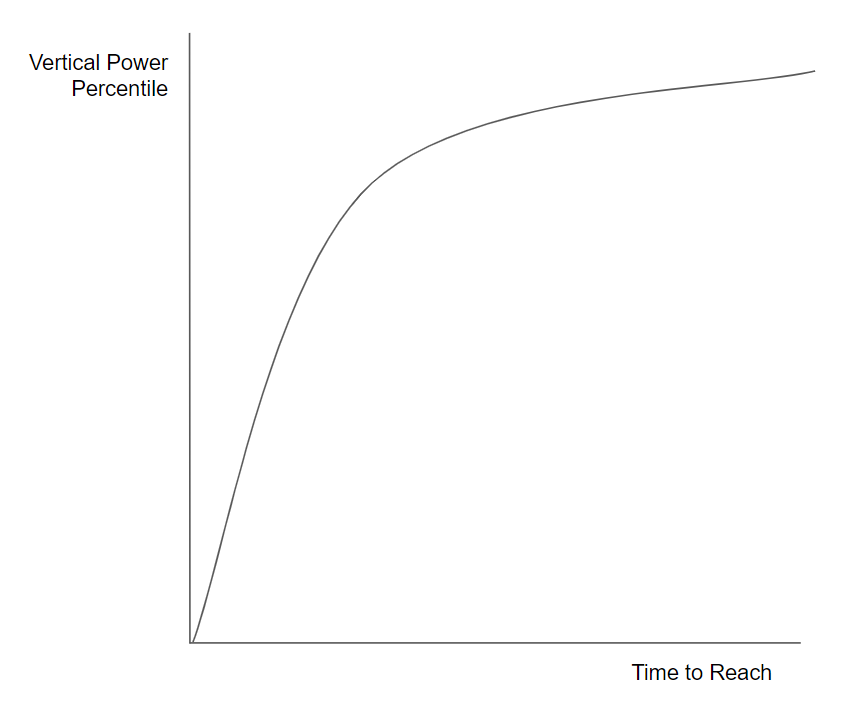
But on another, the returns to time in terms of vertical power percentile decrease (i.e., a given hour or dollar of spend buys less percentile increase as the absolute amount of time/dollar spent increases). It’s easier to go from rank 500 to 400 than rank 100 to 1.
The Seat of Power
Most 4x games revolve around a “seat of power.” Players band together to control the seat, with a single representative from the clan executing against the clan’s interests when on the seat. In some sense, this creates a fixed supply of “victory”: there can only be a single holder of the seat of power. The seat itself gives the holder a vast array of powers. For example, in March of Empires, ruling players control everything from tax rates to peace shield rules.
Ceilings and Seats
We can imagine the vertical power percentile representing the time and costs to obtain the seat of power. The probability of obtaining the seat of power is conditional on the population size of the shard.
Where:
with
However, there’s an additional design space to consider in managing shards over time. Until now, we’ve considered a static problem: what is the optimal shard size? But given the persistence of shards, we must also consider the design space of merging and re-filling shards.
Consider a round-robin style model: new players are assigned shards from a looping list. This ensures a consistent influx of immigration, but players entering elder shard face difficult prospects. By then, top players have accumulated massive amounts of capital.
A former colleague suggested an alternative model: “shard bursting,” or filling up shards in a series, i.e., the following 6,000 new players might all be assigned to shard “A” while the next 6,000 are assigned shard “B.” Bursting hedges against the “round-robin” model by creating a relatively even start line from which players rush to the seat of power. On the flip side, brutal early retention funnels (sub 20% D1 retention) leave bursted shards looking something like modern Japan. With no fresh blood, the shard population will dwindle over time.
I’m not actually sure which model produces the most robust retention rates, maybe we should auction the whole thing off! But I do know the problem is here to stay, and the open economies of web3 only complicate the dynamics. Web3 4x designers certainly have a curious task at hand!
- Page 92 for the coinage of the term.